毫无疑问，这会是量子计算领域里的一个里程碑。

9 月 20 日，据《财富》、《金融时报》等多家外媒报道，谷歌已经利用一台 53 量子比特的量子计算机实现了传统架构计算机无法完成的任务，即在世界第一超算需要计算 1 万年的实验中，谷歌的量子计算机只用了 3 分 20 秒。

这是迄今为止表明量子计算机超越传统架构计算机，并走向实用化最为强烈的迹象。虽然相关论文上传至 NASA 后不久即被删除，但还是有眼疾手快的读者及时保存了论文。谷歌是否真的实现了量子霸权？这一实验算不算一个里程碑事件？读者可以去论文中寻找答案。

论文链接：https://drive.google.com/file/d/19lv8p1fB47z1pEZVlfDXhop082Lc-kdD/view

这篇论文的摘要写道：量子计算机的诱人前景在于量子处理器上执行某项计算任务的速度要比经典处理器快指数倍，而根本性的挑战是构建一个能够在指数级规模的计算空间中运行量子算法的高保真度处理器。在这篇论文中，谷歌研究者使用具有可编程超导量子比特的处理器来创建 53 量子比特的量子态，占据了 2^53∼10^16 的状态空间。重复性实验得到的测量值对相应的概率分布进行采样，并利用经典模拟加以验证。

谷歌的量子处理器大约只需 200 秒即可对量子电路采样 100 万次，而当前最优的超级计算机完成同样的任务大约需要 1 万年。这相对于所有已知的经典算法有了巨大的速度提升，是在计算实验任务中实现的量子霸权，预示着下一个万众瞩目的计算范式的到来。

如果读者想要了解量子计算到底是什么，可以看看下面这篇教程，它不需要我们理解量子力学就能有一个整体的理解：

教程地址：https://arxiv.org/abs/1708.03684

研究社区：这会是量子计算领域一个里程碑

谷歌的论文迅速在量子计算研究社区内传播，而「谷歌实现量子霸权」的消息也不胫而走，成为了上周末科学领域的一个重大新闻。在知乎上，有关这一问题的讨论瞬间吸引了 3000 多万次点击。

量子霸权（quantum supremacy）是指量子计算在某些任务上拥有超越所有传统计算机的计算能力。谷歌的研究人员声称已经实现量子霸权，这意味着最新的量子计算机能力已经达到了目前最为强大的超算也无法企及的程度——它可以在 3 分 20 秒内完成特定任务的运算，而目前世界排名第一的超级计算机、美国能源部橡树岭国家实验室的「Summit」执行同样任务需要大约一万年时间。

如何评价谷歌宣称实现量子霸权的研究？量子计算领域杰出科学家、原香港中文大学副教授、现腾讯量子实验室杰出科学家张胜誉在获知消息之后表示，历史上谷歌硬件组一直做得很好，相信谷歌的研究是有真实性的。量子霸权的实现取决于很多因素，重要的是谷歌的确实现了 50 比特以上、各方面参数接近优秀的系统，这一点难能可贵。

不过，张胜誉认为谷歌主张的量子计算双指数发展规律并不太可能实现。

麻省理工学院量子物理博士在读的 @ 少司命 则对于这篇论文进行了简单的解读：

在硬件方面，谷歌家一直用的是超导电路系统，这里是 54 个物理比特 (transmon) 排成阵列，每个比特可以与临近的四个比特耦合在一起，耦合强度可调 (从 0 到大概 40MHz)。

文章最重要的部分，谷歌在多项式时间内实现了对一个随机量子电路的采样，而在已知的经典计算机上需要的时间则非常非常之久，像文中实现的最极端的例子是，对一个 53 比特 20 个 cycle 的电路采样一百万次，在量子计算机上需要 200 秒，而用目前人类最强的经典的超级计算机同样情况下则需要一万年。亦即在这个问题上，量子实现了对经典的超越。*

这里的 cycle 指的是对这些比特做操作的数目，一个 cycle 包含一系列单比特操作和双比特操作，可以近似理解为电路的深度 (circuit depth)。对于最大的电路，即 53 个比特 20 个 cycle 的情况，在量子处理器上做一百万次采样后得到 XEB 保真度大于 0.1% (5 倍置信度)，用时大概 200 秒。而要在经典计算机上模拟的话，因为比特数目很多整个的希尔伯特空间有 2^53~10^16 而且还有那么多电路操作，这已经超出了我们现在超级计算机的能力 (within considerable time)。

就像文中举的另一个例子，用 SFA 算法大概需要 50 万亿 core-hour(大概是一个 16 核处理器运行几亿年吧), 加 10^13 kWh 的能量 (也就是一万亿度电…)，可以想见是多么难的事情了。而量子这个问题上为啥会比经典好也非常容易理解，用到的就是量子运算的并行性，即量子态可以是叠加态可以在多项式时间内遍历整个希尔伯特空间，而经典计算机模拟的话需要的资源则是随着比特数目指数增加的。

当然有没有可能是有些更好的经典采样算法和量子的差不多，只是我们没有找到呢？文中没有给出很直接的回答，他们认为从复杂度分析来讲经典算法总是会随着比特数和 cycle 指数增加的，而且即使未来有一些更好的经典算法，到时候量子的处理器也发展了所以还是会比经典的好。

最后 @ 少司命 认为，我们对于谷歌新研究感到振奋的同时也要保持清醒，我们离着实现量子计算的完全功力还有很远的距离。硬件上有集成化的问题，比如这里的超导比特系统要加微波 control 要谐振腔 readout，比特数目增加后有空间不足和 cross-talk 等各种问题，远远不止我们图中看到的一个小芯片那么简单。再一个比特数多了电路深度大了怎么继续提高保真度也是很大问题，像这篇文章里 53 个比特到第十几个 circuit cycle 时候保真度只有 10 的负二次方量级了，怎么 decorrelate error 实现量子纠错，最终实现容错量子计算等等，这些都是硬件上的挑战。

算法上，除了这里的采样问题（由此延伸的可以解决的问题其实是非常有限的），又有哪些问题是可以证明量子比经典有显著优势的，可不可以设计一些算法使得量子计算机能解决经典不能解决的问题，或者量子比经典有显著的加速，就像文章最后所说的：

在 NISQ(noisy-intermediate scale quantum computer) 的时代 (如下图)，虽然我们离绿色真正的容错通用量子计算机还很远，但是现在已经开始进入到蓝色区域相信在未来几年会有一些

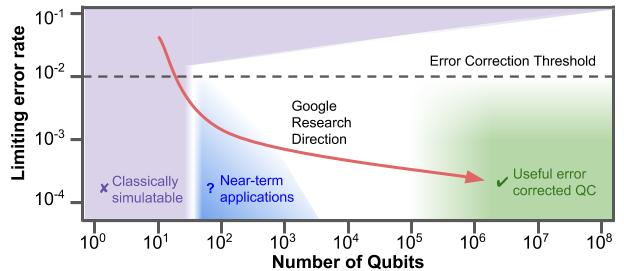
当然，@ 少司命只是表达了自己的看法，至于论文究竟如何，大家还需要自己去读一下。

被 NASA 删除的「量子霸权」论文

以下是谷歌论文《Quantum Supremacy Using a Programmable Superconducting Processor》的大部分内容，供大家参考：

引言

20 世纪 80 年代早期，Richard Feynman 提出，量子计算机将成为解决物理、化学难题的有效工具，因为用传统计算机模拟大规模量子系统的开销呈指数级增长。实现 Feynman 所描述的愿景需要面临理论和实验方面的重大挑战。首先，量子系统能否被设计为一个足够大的计算（希尔伯特）空间来执行计算并且错误率够低、速度够快呢？其次，我们能否提出一个对经典计算机来说很难但对量子计算机来说很容易的问题？谷歌的研究者通过一个超导量子比特处理器在一个新的基准任务中解决了上面两个问题。该实验是迈向量子霸权的一个里程碑事件。

谷歌的研究者通过实验证明，量子加速可以在现实世界的系统中实现，而且不受任何潜在物理定量的限制。量子霸权也预示着有噪声的中等规模量子（Noisy Intermediate- Scale Quantum，NISQ）技术的到来。该基准任务可以直接应用于生成可证明的随机数；这种计算能力也可以用于优化、机器学习、材料科学、化学等领域。然而，完全实现量子计算还需要设计具有容错能力的逻辑量子比特。

为了实现量子霸权，研究者在误差校正方面也实现了许多技术突破。他们开发了快速、高保真门，可以在二维量子比特阵列上同时执行。他们使用交叉熵基准（XEB）在组件和系统层面校准了用到的量子计算机，并对其进行了基准测试。最后，他们使用组件级的保真度来准确预测整个系统的性能，进一步表明量子信息在扩展至大型系统时表现与预期一致。

实现量子霸权的计算任务

为了展示量子霸权，研究者在一个伪随机量子电路输出的采样任务中将他们的量子计算机与当前最强的超级计算机进行了比较。随机电路是进行基准测试的一个合理选择，因为它们没有结构，因此可以保证有限的计算难度。研究者通过重复应用单量子比特和双量子比特逻辑运算来设计一组量子比特纠缠的电路。对量子电路的输出进行采样，可以产生一组比特串（bitstring），如 {0000101, 1011100, …}。由于量子干涉，比特串的概率分布类似于激光散射中的光干扰产生的斑点强度模式，因此，一些比特串比其他比特串更容易出现。随着比特数和门循环数量的增加，用经典计算机计算这种概率分布的难度呈指数级增加。

构建和表征高保真的处理器

图 1：Sycamore 量子处理器。a. 该处理器的布局，有 54 个量子比特，每个量子比特用耦合器（蓝色）与四个最近的量子比特相连；b. Sycamore 芯片的光学图像。

研究者设计了一个名为「Sycamore 的」量子处理器，包含一个由 54 个 transmon 量子比特组成的二维阵列，每个量子比特都以可调的方式与周围四个最近邻的量子比特耦合。连接是向前兼容的，使用表层代码进行误差修正。该设备的一个关键系统设计突破是实现高保真的单和双量子比特运算，这不仅是在隔离的情况下，而且在对多个量子比特同时进行门运算的情况下，还能进行实际的计算。

论文将讨论以下要点：

在一个超导电路中，导电电子凝聚成宏观量子态，使电流和电压具有量子物理特性。该量子计算机使用的是 transmon 量子比特，可以看做是 5-7GHz 的非线性超导谐振器。该量子比特被编码为谐振电路的两个最低量子本征态。每个 transmon 有两个控制器：一个用来激发量子比特的微波驱动器，另一个用来调整频率的磁通控制器。每个量子比特被连接到一个用于读取其状态的线性谐振器。

如下图 1 所示，每个量子比特也使用一个新的可调耦合器与周围相邻的量子比特相连。该耦合器的设计可以实现从 0 到 40MHz 的量子间耦合快速调整。由于一个量子比特不能正常工作，该装置其实使用了 53 个量子比特和 86 个耦合器。

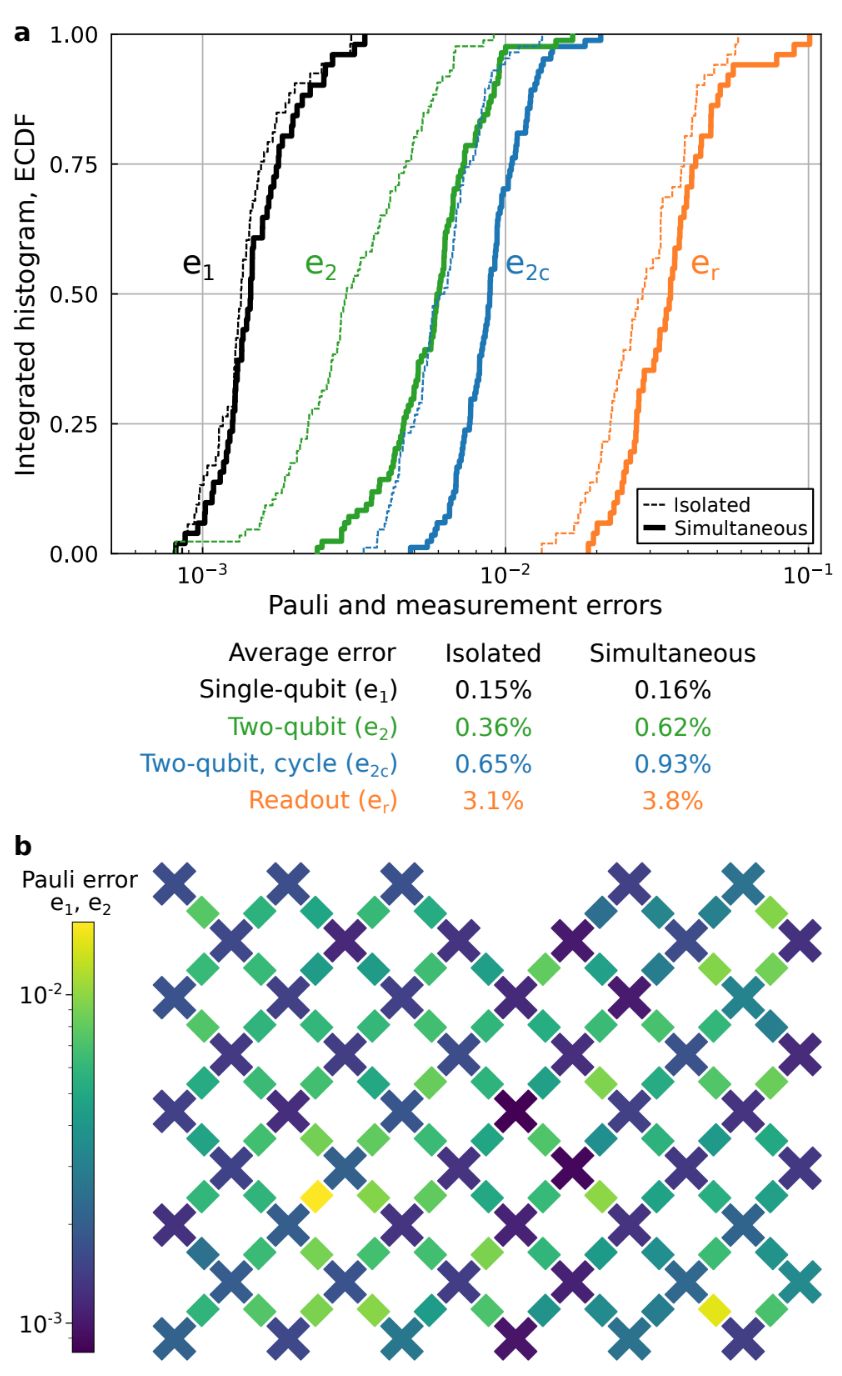
图 2. 系统规模的 Pauli 和测量误差。a.Pauli 误差（黑、绿、蓝）的经验累积分布函数和度数误差（橙）；b. 展示单量子比特和双量子比特 Pauli 误差的热图。

量子霸权的保真度估计

伪随机量子电路生成的门序列（gate sequence）如下图 3 所示。形成「量子霸权电路」的门序列设计用于将创建高度纠缠态（highly entangled state）所需的电路深度最小化，从而保证计算复杂性和经典难度。

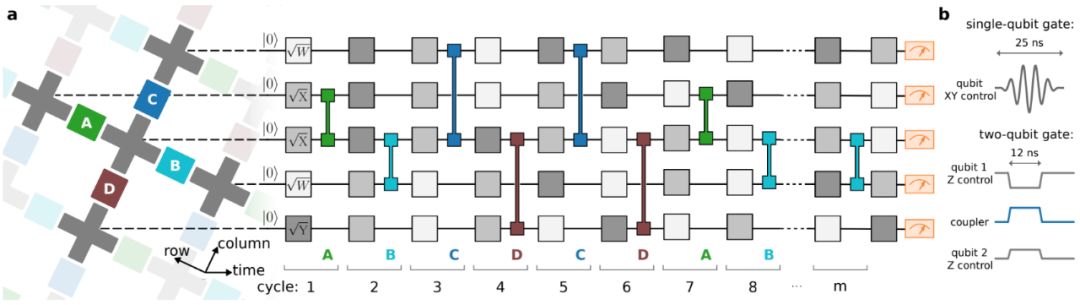
图 3：量子霸权电路的控制操作。a. 实验中使用的量子电路示例；b. 单量子比特和双量子比特门的控制信号波形图。

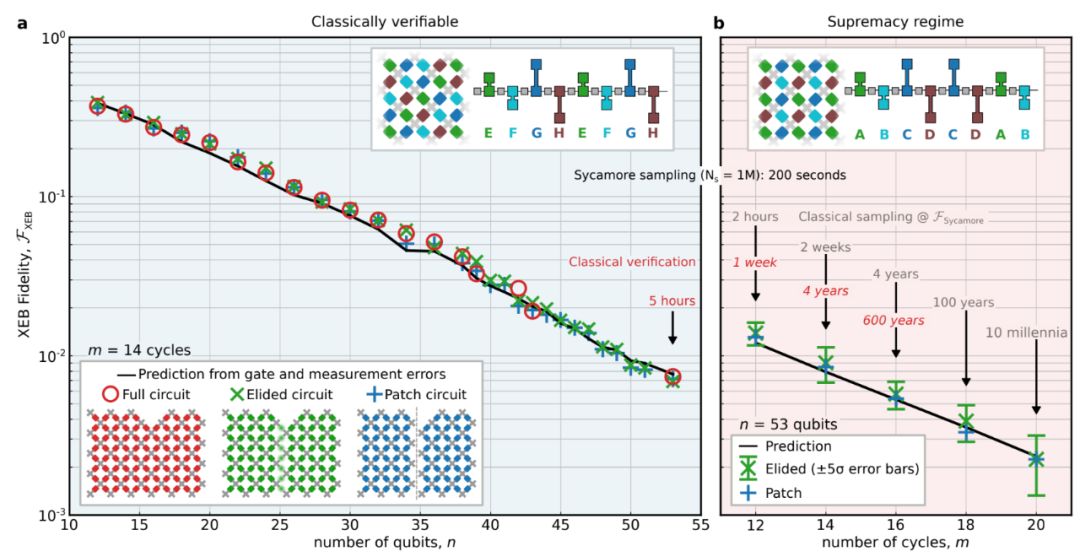
图 4：量子霸权演示。

确定经典计算开销

谷歌研究者模拟了实验中用在经典计算机上的量子电路，这样做是为了实现两个目的：（1）在可能的情况下通过可简化的电路来计算 F_XEB，进而验证量子处理器和基准测试方法（上图 4a）；（2）估算 F_XEB 以及采样硬件电路所需的经典计算开销（上图 4b）。在多达 43 个量子比特的情况下，研究者利用薛定谔算法（SA）来模拟完整量子态的演化，发现 Jülich 超级计算机（10 万核心、250TB）能运行最大的用例。

如果超出 43 量子比特，则没有足够的 RAM 来存储量子态。对于量子比特数量更多的情况，研究者利用薛定谔-费曼混合算法（hybrid Schrödinger-Feynman algorithm，SFA）在谷歌数据中心运行，以计算单个比特串的振幅。SFA 算法将电路分解为两个量子比特块，并在使用一种类似于费曼路径积分的方法将它们连接起来之前，通过薛定谔算法高效地模拟每个量子比特块。虽然 SFA 算法更能节约内存，但随着连接量子比特块的路径和门数量的指数增长，电路深度也相应增加，因而该算法的计算开销也呈指数增加。

在谷歌云服务器上，研究者做出估计，利用 SFA 算法执行 0.1% 保真度的同一任务（m = 20）将花费 50 万亿核心小时（core-hour），消耗 1 拍瓦（petawatt）时的能量。然而，对量子处理器上的电路采样 300 万次只需 600 秒，采样时间受限于控制硬件通信。事实上，量子处理器纯工作时间约为 30 秒。这个最大电路的比特串样本在网络上存档。

人们可能想知道，算法创新能够将经典模拟提高多少。基于复杂性理论，研究者做出假设，该算法任务的开销在 n 和 m 上都是指数级的。的确，过去数年，模拟算法一直在稳步改进。研究者希望最终实现较本文中更低的模拟开销，但预计将始终会被更大量子处理器上的硬件提升所超越。

未来会怎么样？

凡此种种，量子处理器最终实现了量子计算领域的霸权。谷歌研究者期望量子处理器的计算能力可以继续以双指数率增长：模拟量子电路的经典开销随计算体积的增大而增加，并且硬件的提升将有可能遵循量子处理器的摩尔定律，使得计算体积每几年就增大一倍。为了保持双指数增长率并最终提供能够运行 Shor 或 Grover 等已知的量子算法所需的计算体积，量子误差校正工程将成为以后的关注重点。

由 Bernstein 和 Vazirani 制定的「扩展邱奇-图灵论题（Extended Church-Turing Thesis）」声称，图灵机器可以有效地模拟任何「合理的」计算模型。谷歌研究者的实验表明，现在有一种计算模型可能违背了这种说法。他们已经利用物理实现的量子处理器（非常低的误差率）在多项式时间进行随机的量子电路采样，但目前对于经典计算机而言不存在有效的方法。得益于这些进展，量子计算正从一个研究课题过渡到一项能够开发新的计算能力的技术，并且离有价值的短期量子应用只缺少有创造性的算法了。

虽然在实现量子霸权的道路上，谷歌可能已经实现了一个重要的里程碑，但我们和量子计算的黄金时代还有一段距离要走。

参考内容：

https://drive.google.com/file/d/19lv8p1fB47z1pEZVlfDXhop082Lc-kdD/view

https://www.zhihu.com/question/346999432

声明：本文来自机器之心，版权归作者所有。文章内容仅代表作者独立观点，不代表士冗科技立场，转载目的在于传递更多信息。如有侵权，请联系 service@expshell.com。